MAT-HS.F-BF.01
|
MAT-HS Targeted Standards
(F) Concept: Function
(BF) Domain: Building Functions
Cluster: Build a function that models a relationship between two quantities
MAT-HS.F-BF.01 Write a function that describes a relationship between two quantities.
- a. Determine an explicit expression, a recursive process, or steps for calculation from a context.
- b. Combine standard function types using arithmetic operations.
For example, build a function that models the temperature of a cooling body by adding a constant function to a decaying exponential, and relate these functions to the model.
- c. Compose functions.
For example, if T(y) is the temperature in the atmosphere as a function of height, and h(t) is the height of a weather balloon as a function of time, then T(h(t)) is the temperature at the location of the weather balloon as a function of time.
|
Student Learning Targets:
Knowledge Targets
- I can recognize the notation for the composition of functions.
- I can recognize the proper notation for inverse functions.
Reasoning Targets
- I can determine the inverse of a function.
- I can interpret the results of the horizontal line test.
- I can verify whether two functions are inverses of each other using compositions.
Skills (Performance) Targets
- I can graph a linear equation.
- I can manipulate the form of a linear equation.
- I can identify a linear equation.
- I can use algebraic expressions, equations or inequalities involving one or two variables to represent geometric relationships.
- I can perform composition of algebraic functions.
- I can demonstrate the inverse of an algebraic function graphically.
- I can perform the horizontal line test to determine if the inverse of a function exists.
- I can combine function types, such as linear and exponential, using arithmetic operations.
Product Targets
- I can write a functions that describes a relationship between two quantities.
- I can write an explicit or recursive expression or describe the calculations needed to model a function given a situation.
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
Web
|
|
Vocab
- explicit
- recursive
- linear
- exponential
- function
|
|
|
MAT-HS.F-BF.02
|
MAT-HS Targeted Standards
(F) Concept: Function
(BF) Domain: Building Functions
Cluster: Build a function that models a relationship between two quantities
MAT-HS.F-BF.02 Write a function that describes a relationship between two quantities.
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
Skills (Performance) Targets
- I can make connections between linear functions and arithmetic sequences, and exponential functions and geometric sequences.
Product Targets
- I can write and translate between the recursive and explicit formula for a arithmetic sequence and use the formulas to model a situation.
- I can write and translate between the recursive and explicit formula for a geometric sequence and use the formulas to model a situation.
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
Web
|
|
Vocab
- sequence
- arithmetic sequences
- geometric sequences
|
|
|
MAT-HS.F-BF.03
|
MAT-HS Targeted Standards
(F) Concept: Function
(BF) Domain: Building Functions
Cluster: Build new functions from existing functions.
MAT-HS.F-BF.03* Identify the effect on the graph of replacing f(x) by f(x) + k, f(x + k), k f(x), and f(kx), for specific values of k (both positive and negative); find the value of k given the graphs. Recognize even and odd functions from their graphs.
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
Skills (Performance) Targets
- I can experiment to identify, using technology, the transformational effects on the graph of a function f(x) when f(x) is replaced by f(x)+k, k∙f(x), f(kx), and f(x+k) for specific values of k, both positive and negative.
- I can find the value of k given the graph of a transformed function.
- I can recognize even and odd functions from their graphs and equations.
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
|
4.0
(advanced)
|
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
Write three different quadratic functions whose graphs have the line x = 4 as an axis of symmetry but have different y-intercepts. |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
|
3.0
(proficient)
|
The student can:
- analyze the transformational effects on the graph of a function.
- find the value of k given the graph of a transformed function.
- determine whether a function is even or odd given a graph.
The student exhibits no major errors or omissions.
|
Describe all the transformations and graph the function.

|
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
|
2.0
(progressing)
|
There are no major errors or omissions regarding the simpler details and processes as the student can:
- recognize and recall specific terminology, such as:
- vertical shift
- horizontal shift
- compress/amplified
- stretch/shrink
- reflection
- even function
- odd function
However, the student exhibits major errors or omissions regarding the more complex ideas and processes. |
Given the graph, identify all of the transformations.
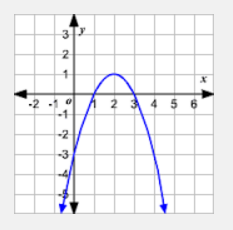
|
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
|
1.0
(beginning)
|
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
|
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
|
Resources
| Web |
|
Vocab
- transformation
- even functions
- odd functions
|
|
|
MAT-HS.F-BF.04
|
MAT-HS Targeted Standards
(F) Concept: Function
(BF) Domain: Building Functions
Cluster: Build new functions from existing functions
MAT-HS.F-BF.04 Find inverse functions.
- a. Solve an equation of the form f(x) = c for a simple function f that has an inverse and write an expression for the inverse.
For example, f(x) =2 x³ or f(x) = (x+1)/(x-1) for x ≠ 1.
- b. Verify by composition that one function is the inverse of another.
- c. Read values of an inverse function from a graph or a table, given that the function has an inverse.
- d. Produce an invertible function from a non-invertible function by restricting the domain.
|
Student Learning Targets:
Knowledge Targets
- I can recognize the notation for the composition of functions.
- I can recognize the proper notation for inverse functions.
Reasoning Targets
- I can determine the inverse of a function.
- I can interpret the results of the horizontal line test.
- I can verify whether two functions are inverses of each other using compositions.
Skills (Performance) Targets
- I can perform composition of algebraic functions.
- I can demonstrate the inverse of an algebraic function graphically.
- I can perform the horizontal line test to determine if the inverse of a function exists.
- I can find the inverse of a given function.
- I can solve a function for the dependent variable and write the inverse of a function by interchanging the dependent and independent variables.
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
Web
|
|
Vocab
- inverse function
- independent variable
- dependent variable
|
|
|
MAT-HS.F-BF.05
|
MAT-HS Targeted Standards
(F) Concept: Function
(BF) Domain: Building Functions
Cluster: Build new functions from existing functions
MAT-HS.F-BF.05 Understand the inverse relationship between exponents and logarithms and use this relationship to solve problems involving logarithms and exponents.
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
Skills (Performance) Targets
Product Targets
|
Alg II Solve Logarithmic Equations Proficiency Scale
| Score |
|
Description |
Sample Activity
|
|
4.0
(advanced)
|
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
Describe and correct the error in this work:
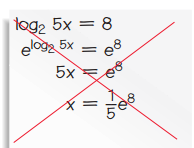
|
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
|
3.0
(proficient)
|
The student can:
- solve a logarithmic equation and recognize an extraneous solution.
The student exhibits no major errors or omissions. |
Solve the following logarithmic equation and check for extraneous solutions:
log3(x2-30)=log3(x)
Solve the following logarithmic equation and check for extraneous solutions:
2log2(x)=log2(4)+log2(x-1)
|
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
|
2.0
(progressing)
|
There are no major errors or omissions regarding the simpler details and processes as the student can:
- recognize and recall specific terminology such as:
- Base
- Logarithm
- Exponentiate
- Condense
- Expand
- solve simple logarithmic equations.
- evaluate a logarithmic expression.
- use properties of logarithms to expand and condense an expression.
However, the student exhibits major errors or omissions regarding the more complex ideas and processes.
|
Solve the following logarithmic equation for x:
log10(100)=x |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
|
1.0
(beginning)
|
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.F-IF.01
|
MAT-HS Targeted Standards
(F) Concept: Function
(IF) Domain: Interpreting Functions
Cluster: Understand the concept of a function and use function notation.
MAT-HS.F-IF.01 Understand that a function from one set (called the domain) to another set (called the range) assigns to each element of the domain exactly one element of the range. If f is a function and x is an element of its domain, then f(x) denotes the output of f corresponding to the input x. The graph of f is the graph of the equation y = f(x).
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
Skills (Performance) Targets
- I can use the definition of a function to determine whether a relationship is a function given a table, graph or words.
- I can identify x as an element of the domain and f(x) as an element in the range given the function f.
- I can identify that the graph of the function f is the graph of the function y=f(x).
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
|
4.0
(advanced)
|
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |

|
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
|
3.0
(proficient)
|
The student can:
-
understand that a function from one set (called the domain) to another set (called the range) assigns to each element of the domain exactly one element of the range. If f is a function and x is an element of its domain, then f(x) denotes the output of f corresponding to the input x. The graph of f is the graph of the equation y = f(x).
The student exhibits no major errors or omissions.
|
Is the relation a function (yes or no)? Explain.
a.

b.
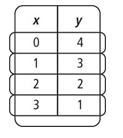
Identify the domain and range of the relation. Is this relation a function (yes or no)? Explain.
(-2, 0.5), ( 0,2.5), (4,6.5), (5,2.5)
Graph
f (x) = 2x + 2
|
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
|
2.0
(progressing)
|
There are no major errors or omissions regarding the simpler details and processes as the student:
- Recognize and recall basic vocabulary such as:
- range
- domain
- relation
- function notation
- vertical line test
However, the student exhibits major errors or omissions regarding the more complex ideas and processes.
|
Find the range of the relation.(4, -2), (-2, 3), (1, -3).
Find the domain of the relation.
(2, 4), (8, 11), (9, 1), (4, 2)
Does the relation pass a vertical line test?

- Identify the domain and range for the given set of ordered pairs. Is this relation a function?(7,2), (-1,4), (2,-2), (-6,5), (0,0)
|
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
|
1.0
(beginning)
|
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.F-IF.02
|
MAT-HS Targeted Standards
(F) Concept: Function
(IF) Domain: Interpreting Functions
Cluster: Understand the concept of a function and use function notation.
MAT-HS.F-IF.02 Use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context.
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
Skills (Performance) Targets
- I can evaluate functions for inputs in their domains.
- I can interpret statements that use function notation in terms of a context in which they are used.
- I can use f(x) notation when a relation is determined to be a function.
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
|
4.0
(advanced)
|
In addition to achieving level 3.0 content, the student makes in-depth inferences and applications that go beyond what was taught |
-
If f(x) = –5x + 11 and f(n) = 21, what is the value of n? Explain.
-
Each set of ordered pairs represents a function. Write a rule that represents the function:
-
(-2, 10/9), (-1, 4/3), (0,2),(1,4)(2,10)
|
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
|
3.0
(proficient)
|
The student:
Can use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context.
The student exhibits no major errors or omissions. |
-
What is f(–5) for the function f(x) = –9x – 3?
-
Find the range of each function for the given domain. f(x) = x3 + 1; {–2, –1, 0, 1, 2}
-
In the formula d(t) = rt, explain what r represents, what t represents, and what d(t) represents.
- How can it be determined if a relation is a function?
|
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
|
2.0
(progressing)
|
There are no major errors or omissions regarding the simpler details and processes as the student:
Can use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context.
Recognize and recall basic vocabulary such as:
-
Domain
-
Range
-
Function vs. Relation
-
Function Notation
However, the student exhibits major errors or omissions regarding the more complex ideas and processes. |
-
Find the range of the function for the given domain.
-
f (x) = –2x + 1; {–2, 0, 2, 4, 6}
-
Evaluate f(x) = 2x +3 for x = 6
|
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
|
1.0
(beginning)
|
With help, a partial understanding of some of the simpler details and processes and some of the more complex ideas and processes. |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
Web
- Function Notation WS:
- Function Notation WS 2:
|
|
Vocab
|
|
|
MAT-HS.F-IF.03
|
MAT-HS Targeted Standards
(F) Concept: Function
(IF) Domain: Interpreting Functions
Cluster: Understand the concept of a function and use function notation.
MAT-HS.F-IF.03 Recognize that sequences are functions, sometimes defined recursively, whose domain is a subset of the integers.
For example, the Fibonacci sequence is defined recursively by f(0) = f(1) = 1, f(n+1) = f(n) + f(n-1) for n ≥ 1. |
Student Learning Targets:
Knowledge Targets
- I can recognize that sequences are functions, sometimes defined recursively, whose domain is a subset of the integers.
Reasoning Targets
Skills (Performance) Targets
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.F-IF.04
|
MAT-HS Targeted Standards
(F) Concept: Function
(IF) Domain: Interpreting Functions
Cluster: Interpret functions that arise in applications in terms of the context
MAT-HS.F-IF.04* For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship.
Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity. |
Student Learning Targets:
Knowledge Targets
- I can identify key features in graphs and tables to include intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity for a given function.
Reasoning Targets
Skills (Performance) Targets
- I can use correct notation when identifying key features of graphs and tables.
Product Targets
- I can sketch the graph of a function given its key features.
|
Alg II Key Features of Graphs Proficiency Scale
| Score |
|
Description |
Sample Activity
|
|
4.0
(advanced)
|
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
Given the graph, identify the intervals where both functions are increasing.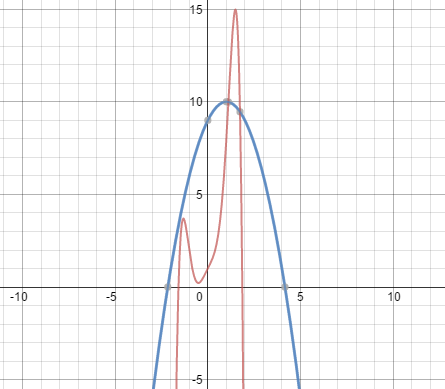
|
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
|
3.0
(proficient)
|
The student can:
- identify key features in graphs and tables including intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; domain and range; and periodicity for a given function.
- sketch the graph of a function given its key features.
The student exhibits no major errors or omissions.
|
Identify the following from the graph:

x-intercepts:
y-intercepts:
Increasing Intervals:
Decreasing Intervals:
Positive Intervals:
Negative Intervals:
Maximums:
Minimums:
Domain:
Range:
Sketch a function that would have an increasing interval from (3,+∞) and a relative minimum at (3,4).
|
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
|
2.0
(progressing)
|
There are no major errors or omissions regarding the simpler details and processes as the student can:
- Recognize and recall specific terminology such as:
- intervals
- intercept (x and y)
- relative minimum and maximum
- periodicity
- end behavior
- symmetry
- increasing
- decreasing
- use interval notation accurately.
However, the student exhibits major errors or omissions regarding the more complex ideas and processes. |
Write the following in interval notation:
x<3
x>5
x≥10
5<x≤9

For the graph given, the function is increasing from________ to -1 and 3 to _______.
|
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
|
1.0
(beginning)
|
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
|
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
|
Resources
|
Web
|
|
Vocab
- intercepts
- relative maximum
- relative minimum
- end behavior
- periodicity
- symmetry
|
|
|
MAT-HS.F-IF.05
|
MAT-HS Targeted Standards
(F) Concept: Function
(IF) Domain: Interpreting Functions
Cluster: Interpret functions that arise in applications in terms of the context
MAT-HS.F-IF.05 Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes.
For example, if the function h(n) gives the number of person-hours it takes to assemble n engines in a factory, then the positive integers would be an appropriate domain for the function. |
Student Learning Targets:
Knowledge Targets
Reasoning Targets
Skills (Performance) Targets
- I can solve a linear system (substitution, linear combination, graphically).
- I can write a linear system.
- I can identify the number of solutions of a linear system.
- I can identify the most efficient method to solve a system.
- I can check the solution of the system.
- I can graph a linear equation.
- I can manipulate the form of a linear equation.
- I can identify a linear equation.
- I can interpret a graph to determine the appropriate numerical domain being described.
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|

