MAT-HS.G-CO.01
|
MAT-HS Targeted Standards
(G) Concept: Geometry
(CO) Domain: Congruence
Cluster: Experiment with transformations in the plane.
MAT-HS.G-CO.01 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc.
|
Student Learning Targets:
Knowledge Targets
- I can understand and use definitions of angle, circle, perpendicular lines, parallel lines, and line segment based on the undefined notions of point, line, distance along a line, and length of an arc.
Reasoning Targets
Skills (Performance) Targets
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.G-CO.02
|
MAT-HS Targeted Standards
(G) Concept: Geometry
(CO) Domain: Congruence
Cluster: Experiment with transformations in the plane
MAT-HS.G-CO.02 Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch).
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
- I can compare transformations that preserve distance and angle measure to those that do not.
Skills (Performance) Targets
- I can use transformations to graph linear, quadratic and absolute value functions.
- I can represent rigid and size transformations of figures in a coordinate plane.
- I can describe transformations (to include translations and horizontal and vertical stretching) on a set of points as inputs to produce another set of points as outputs.
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.G-CO.03
|
MAT-HS Targeted Standards
(G) Concept: Geometry
(CO) Domain: Congruence
Cluster: Experiment with transformations in the plane
MAT-HS.G-CO.03 Given a rectangle, parallelogram, trapezoid, or regular polygon, describe the rotations and reflections that carry it onto itself.
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
Skills (Performance) Targets
- I can describe the rotations and reflections of a rectangle, parallelogram, trapezoid, or regular polygon that map each figure onto itself.
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.G-CO.04
|
MAT-HS Targeted Standards
(G) Concept: Geometry
(CO) Domain: Congruence
Cluster: Experiment with Transformations in the plane.
MAT-HS.G-CO.04 Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines, and line segments.
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
Skills (Performance) Targets
- I can develop the meaning of rotations, reflections, and translations based on angles, circles, perpendicular lines, parallel lines, and line segments.
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.G-CO.05
|
MAT-HS Targeted Standards
(G) Concept: Geometry
(CO) Domain: Congruence
Cluster: Experiment with transformations in the plane
MAT-HS.G-CO.05 Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another.
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
Skills (Performance) Targets
- I can create a sequence of transformations that maps a given geometric figure onto another.
Product Targets
- I can draw the transformation (rotation, reflection, or translation) of a geometric figure using a variety of methods.
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.G-CO.06
|
MAT-HS Targeted Standards
(G) Concept: Geometry
(CO) Domain: Congruence
Cluster: Understand congruence in terms of rigid motions
MAT-HS.G-CO.06 Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if they are congruent.
|
Student Learning Targets:
Knowledge Targets
- I can define congruent.
- I can define similarity.
- I can match corresponding sides in two or more figures.
- I can match corresponding angles in two or more figures.
- I can identify types of transformations such as translation, rotation, and reflection.
- I know that a translation is a slide.
- I know that a rotation is a turn.
- I know that a reflection is flip.
- I can illustrate transformations on a coordinate plane.
- I can plot points/ordered pairs on a coordinate plane.
- I can use the fact that rigid transformations preserve size and shape to connect the idea and definition of congruence.
Reasoning Targets
- I can compare figures to determine if they are congruent.
- I can compare figures to determine if they are similar.
- I can use a proportion to solve the unknown side or angle of a shape.
- I can use a ratio to compare the side lengths or angles of a shape.
- I can predict the coordinates of a transformed figure.
- I can find the scale factor of two similar figures when given the dimensions.
- I can use descriptions of rigid motion and transformed geometric figures to predict the effects rigid motion has on figures in the coordinate plane.
Skills (Performance) Targets
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.G-CO.07
|
MAT-HS Targeted Standards
(G) Concept: Geometry
(CO) Domain: Congruence
Cluster: Understand congruence in terms of rigid motions
MAT-HS.G-CO.07 Use the definition of congruence in terms of rigid motions to show that two triangles are congruent if and only if corresponding pairs of sides and corresponding pairs of angles are congruent.
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
- I can determine congruence and similarity among geometric objects.
- I can use similarity or congruence to solve for a missing side/angle.
Skills (Performance) Targets
- I can use the definition of congruence, based on rigid motion, to show two triangles are congruent if and only if their corresponding sides and corresponding angles are congruent.
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
|
Advanced
|
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
|
Proficient
|
The student can:
· show two figures are congruent after a sequence of rigid motions (translations, reflections, rotations).
· use the definition of congruence as a test to see if two figures are congruent (if and only if they have the same shape and size).
|
-A student finds two triangles on two different pieces of patty paper. He places them on the desk to compare them. He slides and then turns the paper so that the two triangles on are on top of each other and then he notices that he needs to flip one of the papers so that they will land exactly on top of each other. The student concludes that they are copies of each other. Mathematically, what did this procedure prove about the triangles? |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
|
Progressing
|
There are no major errors or omissions regarding the simpler details and processes as the student can:
· recognize and recall terminology to answer questions.
· use composite transformations to map one figure onto another.
· recognize the effects of rigid motion on orientation and location of a figure.
|
1. A rigid motion is the same as:
A) A mapping
B) A transformation
C) An Isometric transformation
D) A proportional expansion
2. Congruence can be found through isometric transformations because they preserve key characteristics of the shape. Which of the following is NOT one of the characteristics that an isometry preserves?
A)Angle size
B) Location on the plane
C)Distance between points
D) Collinearity of points
3. K(x,y) - - - - - > (-x,-y)could represent a transformation that could establish congruence. T or F
|
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
|
Beginning
|
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.G-CO.08
|
MAT-HS Targeted Standards
(G) Concept: Geometry
(CO) Domain: Congruence
Cluster: Understand congruence in terms of rigid motions
MAT-HS.G-CO.08 Prove two triangles are congruent using the congruence theorems such as ASA, SAS, and SSS.
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
- I can determine congruence and similarity among geometric objects.
- I can use similarity or congruence to solve for a missing side/angle.
Skills (Performance) Targets
- I can use the definition of congruence, based on rigid motion, to explain the triangle congruence criteria; ASA, SSS, and SAS.
Product Targets
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
|
Advanced
|
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations.
- The student will be able to explain why triangles in a three dimensional figure are congruent.
- The student will be able to prove statements by first proving congruent triangles.
- The student will be able to explain why AA or SSA gives you congruent triangles only sometimes.
|
-

|
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
|
Proficient
|
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations.
The student can perform all the actions for each concept listed below:
|
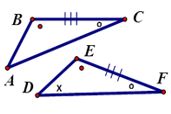
Jennifer states that ∆ABC ≅ ∆DEF can be proven by either ASA or AAS. Joshua disagrees – he says it can only be done by ASA because in ∆ABC it is missing the matching symbol to ∠D so we do not know if ∠A ≅ ∠D. Who is correct? Explain.
|
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
|
Progressing
|
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content).
- The student can recognize and recall terminology to answer questions.
|
 
|
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| Beginning |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.G-CO.09
|
MAT-HS Targeted Standards
(G) Concept: Geometry
(CO) Domain: Congruence
Cluster: Prove geometric theorems
MAT-HS.G-CO.09 Prove and apply theorems about lines and angles.
Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints. |
Student Learning Targets:
Knowledge Targets
Reasoning Targets
Skills (Performance) Targets
- I can prove theorems pertaining to lines and angles.
- I can prove vertical angles are congruent.
- I can prove when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent.
- I can prove points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints.
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| 4.0 |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations. |
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| 3.0 |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations. |
- |
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| 2.0 |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content). |
- |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| 1.0 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|
MAT-HS.G-CO.09.a |
MAT-HS Targeted Standards
(G) Concept: Geometry
(CO) Domain: Congruence
Cluster: Prove geometric theorems
MAT-HS.G-CO.09.a Prove theorems about lines and angles.
Theorems include but are not limited to: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints.
|
Student Learning Targets:
Knowledge Targets
Reasoning Targets
Skills (Performance) Targets
Product Targets
|
Proficiency Scale
| Score |
|
Description |
Sample Activity
|
| Advanced |
In addition to Score 3.0, the student demonstrates in-depth inferences and applications regarding more complex material that go beyond end of instruction expectations.
Concepts:
Vertical Angles
Angles created by parallel lines and a transversal
Perpendicular Bisector theorems
|
- |
| |
3.5 |
In addition to Score 3.0 performance, the student demonstrates in-depth inferences and applications regarding the more complex content with partial success. |
| Proficient |
“The Standard.” The student demonstrates no major errors or omissions regarding any of the information and processes that were end of instruction expectations.
- Identify relevant given information
- Arrange reasoning in a logical sequence
- Support reasoning using appropriate justifications (theorems, postulates, definitions, etc.)
Concepts:
Vertical Angles
Angles created by parallel lines and a transversal
Perpendicular Bisector theorems
|

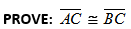
|
| |
2.5 |
The student demonstrates no major errors or omissions regarding the simpler details and processes (Score 2.0 content) and partial knowledge of the more complex ideas and processes (Score 3.0 content). |
| Progressing |
The student demonstrates no major errors or omissions regarding the simpler details and processes but exhibits major errors or omissions regarding the more complex ideas and processes (Score 3.0 content).
- partially prove but reasoning has gaps, steps missing, incorrect reasoning, etc.
- recall theorems, definitions, and postulates
- fill out justification given a statement
Concepts:
Vertical Angles
Angles created by parallel lines and a transversal
Perpendicular Bisector theorems
|
 |
| |
1.5 |
The student demonstrates partial knowledge of the simpler details and processes (Score 2.0 content) but exhibits major errors or omissions regarding the more complex ideas and procedures (Score 3.0 content). |
| Beginning |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) and some of the more complex ideas and processes (Score 3.0 content). |
- |
| |
0.5 |
With help, the student demonstrates a partial understanding of some of the simpler details and processes (Score 2.0 content) but not the more complex ideas and processes (Score 3.0 content). |
| 0.0 |
Even with help, the student demonstrates no understanding or skill. |
- |
Resources
|
|

